Hanoiiwa

Robots today must be able to engage in autonomous task planning as well as motion planning to solve challenges. In this project, I present Hanoi-iiwa, a robotic system that is able to solve the Tower of Hanoi puzzle. With the goal of solving the puzzle correctly and efficiently, I built the system Drake and used a KUKA LBR iiwa robot arm. The system has a recursive Tower of Hanoi solver, a grasp position and posture selector, and a motion planner as its core components. I evaluated the performance of this system in terms of its correctness, efficiency, and robustness. The results show that the system is able to successfully solve the 3-disk Tower of Hanoi puzzle 100% of the time within 180 seconds over 10 runs.

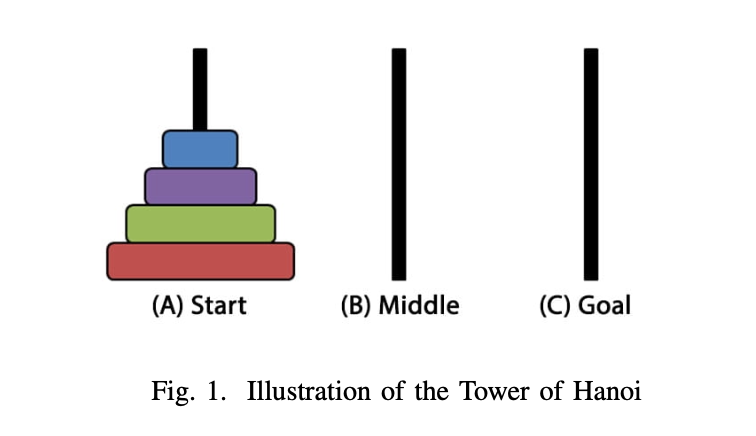
II. RELATED WORK The Tower of Hanoi is a classic mathematical puzzle played around the world. The objective of the game is to stack all disks on the target peg in order of decreasing diameter. The robot’s movement is subject to two constraints: 1) Only one disk can be moved at a time. 2) A larger disk cannot be placed on top of a smaller disk. The standard setup of a 4-disk Tower of Hanoi puzzle is presented in Fig. 1. At the beginning of the puzzle, four disks Fig. 1. Illustration of the Tower of Hanoi are stacked on peg (A). While the middle peg (B) can be used as a temporary holding place, the puzzle is solved when all disks are stacked in the same order on peg (C). The Tower of Hanoi is a puzzle with exponential time complexity [5], and much research has been done on solving the Tower of Hanoi in the field of mathematics, computer science, and robotics.

A. Recursive Approach to The Tower of Hanoi As a widely studied algorithm challenge for new program- mers, the Tower of Hanoi puzzle with n disks would require at least 2n − 1 moves to solve [6]. Different forms of solutions have been proposed by mathematicians, such as iterative solutions [6], recursive solutions [8], and binary solutions. Our project will combine the classic recursive approach of solving the puzzle with robotic manipulation techniques, demonstrating its ability to not only reason through the puzzle, but also solve the puzzle physically. We choose to implement the recursive algorithm as it provides a compact solution with great flexibility for the robot to play the Tower of Hanoi with any number of disks.

B. Path Planning for Disk Transportation A critical challenge for a robot to solve the Tower of Hanoi is to determine a smooth, collision-free and time-efficient path to transport each disk to desired pegs. In 2013, a physical system with two robotic manipulators capable of solving variations of the Tower of Hanoi has been developed by Havur et al. [4]. Havur’s system approached the problem of path planning by establishing a bilateral relationship between task planning and motion planning in the framework [4]. Havur employed Rapidly exploring Random Trees (RRT) [7] using both the initial and the goal location as starting nodes of the bilateral RRT [4]. Bilateral RRT expands from both starting nodes to the center, and a desired trajectory is created once paths of two ends connect [4].

Path planning in our project differs from the approach taken by Havur in several critical ways. First, our robot assumes an initial knowledge of the starting location of each disk and peg. We made this simplification given the limited time of our project. With more time, a camera system can be installed to determine the location of disks and pegs dynamically using point cloud registration [8]. Second, instead of RRT, we generate the gripper’s planned path by a simple linear interpolation of keyframes, which we implement using Drake’s PiecewisePolynomial class. We choose this implementation because the manipulation environment of the Tower of Hanoi is static and has no cluttered objects, and simple interpolation is sufficient to generate efficient collision-free trajectories and has less computational complexity compared to RRT. Our choice is further justified by our decision to use flat platforms of different colors to represent pegs, which reduces the required accuracy of the robot’s positioning of the disks and allows more flexibility in generating feasible paths to use interpolation.

C. Limitations of Current Research and Goal of Our Project The goal of our research is to build a robotic system capable of strategic task planning and path planning in the context of playing the Tower of Hanoi. Compared to complex physical robotic systems like Havur’s, our system takes on a fundamental approach and is nonetheless efficient in solving a slightly simplified version of the problem. We constructed a system composed of a recursive puzzle solver, a gripper grasp position selector, and a robot arm motion planner. The system was tested on a simulation Tower of Hanoi model with three disks, and results showed that it was capable of solving a 3- disk Tower of Hanoi puzzle with a 100% success rate on 10 runs. With minor modifications, the system can be expanded to solve the Tower of Hanoi puzzles with more than three disks easily. We made certain simplifications on visual components of the model and the environment as trade-offs to present a functioning system given the limited amount of time. The final product of our project is Hanoi-iiwa, a working implementa- tion of a robot The Tower of Hanoi solver. Thanks to Drake’s wide range of compatible robot models, the system of Hanoi- iiwa can be generalized to control different types of robot arms.

To develop Hanoi-iiwa, we followed three steps: First, we set up the simulation environment in Drake; Second, we designed the system architecture with three components of a puzzle solver, a grasp selector, and a motion planner; Last, we implemented the system and optimized its performance.

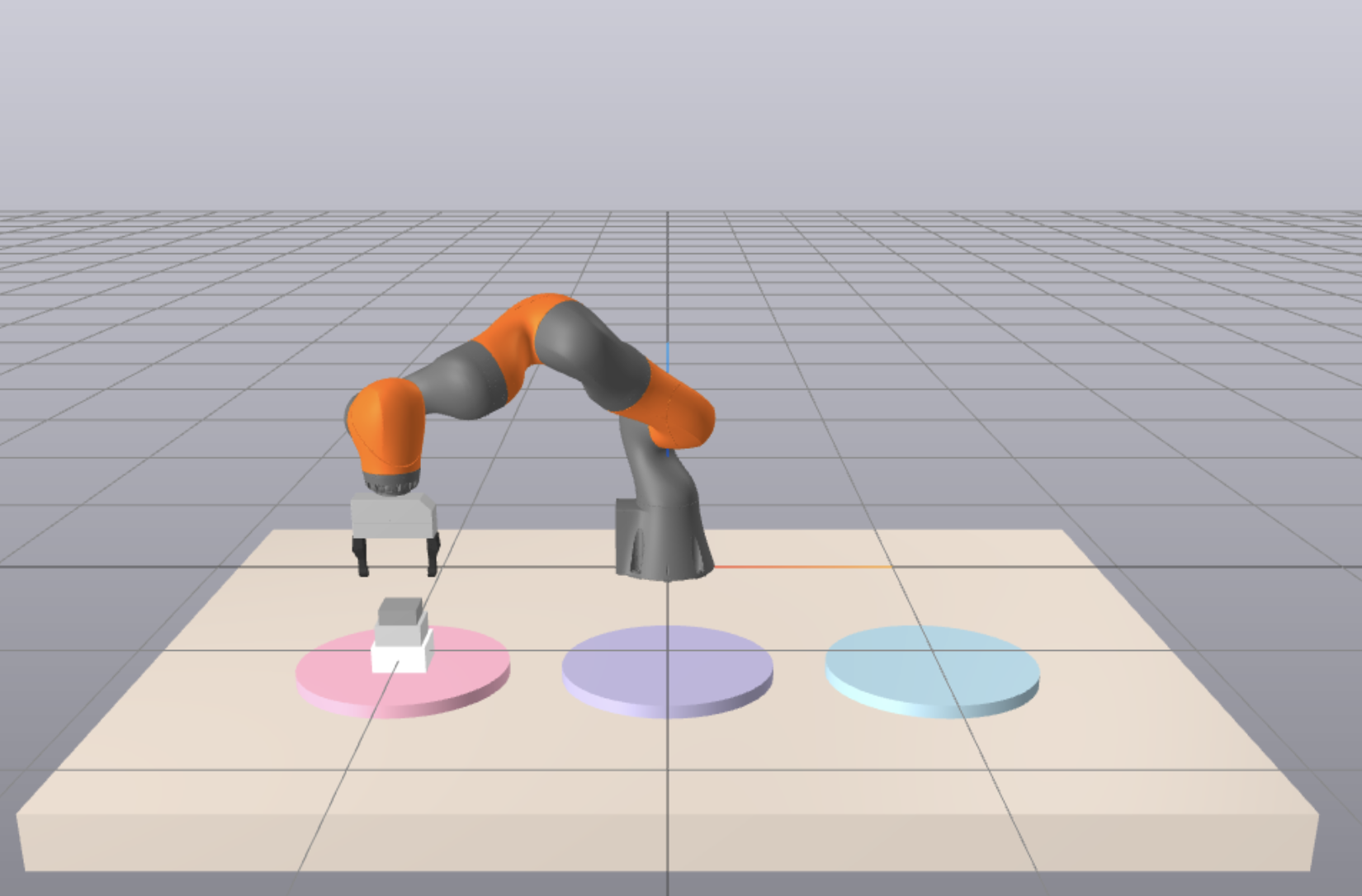
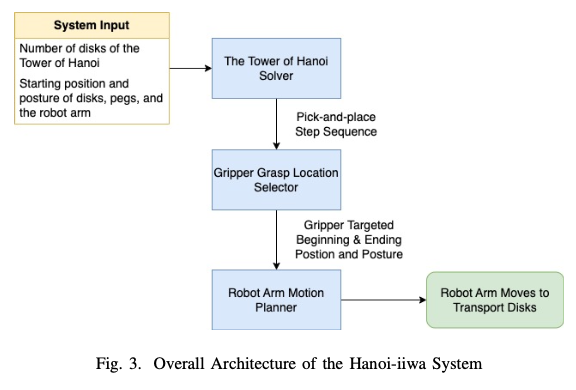
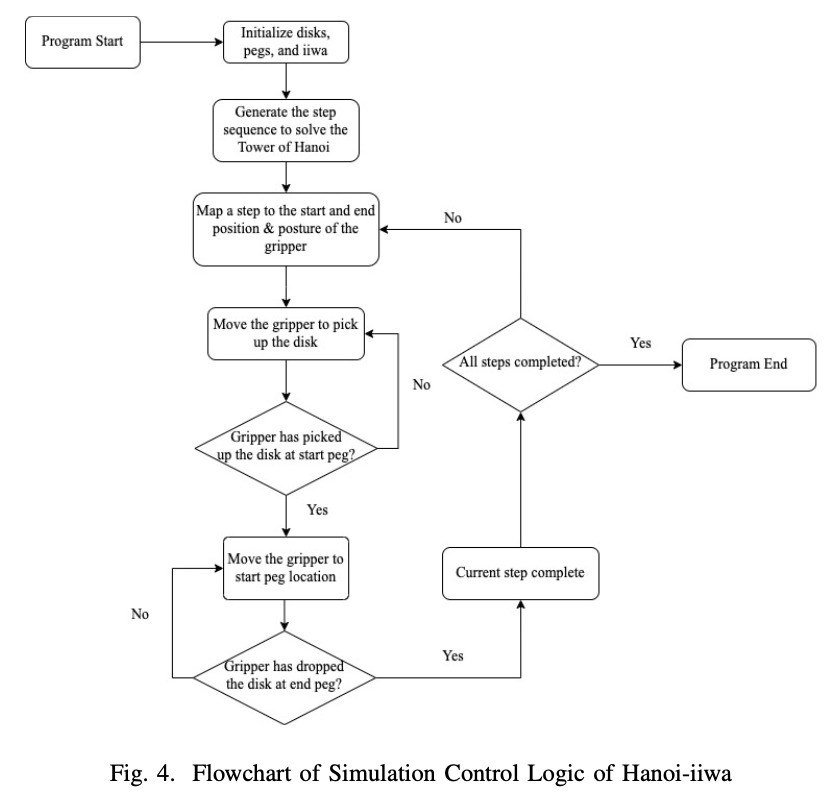
A. Simulation Environment Setup The simulation environment of Hanoi-iiwa is composed of a KuKa LBR iiwa robot arm, three ”pegs” of the Tower of Hanoi in the form three cylindrical platforms of different colors, and three ”disks” represented by boxes of different sizes. The 3D visualization of Hanoi-iiwa in Drake is shown in Fig. 1 below. Fig. 2. Setup of Hanoi-iiwa in Drake Due to the difficulty of contact geometry with objects with holes, we could not simulate the three pegs in the original tower of Hanoi game with loops that have holes in the middle. Instead, we replaced the peg in the original model with colored areas indicating the spot and the disks with boxes that increase in size. Moreover, instead of perceiving the location and pose of the disks at every grasp which is time consuming and data- heavy, we simply store the pose of each disk in a list of variables and update it when it is moved. Therefore we have access to the location of any disk in time. Our project is based on the Drake simulation platform and we referenced the Drake guide extensively. Specifically, we used the AddShape function in Drake to build the disks that have increasing diameters. B. System Architecture Design At a high level, a recursive Tower of Hanoi solver, a gripper grasp position and posture selector, and a motion planner are the three core components of the Hanoi-iiwa system. As shown in Fig. 3, the system accepts the number of disks in the Tower of Hanoi, the starting position and posture of disks, pegs, and the robot arm as input. The puzzle solver takes the input and generates a sequence of pick-and-place movement steps, where each step specifies the disk to be moved, the starting peg, and the destination peg. For each step in the sequence, the gripper grasp position selector maps the step to the desired beginning and ending position and rotation of the robot’s gripper. Finally, the motion planner takes the data and constructs a trajectory for the gripper using key frame interpolation, derives joint angles of the robot arm at each time step of the trajectory.

We evaluate the performance of Hanoi-iiwa based on its ability to successfully solve the Tower of Hanoi and the efficiency of its solution. Due to the limitation of time and exponential time complexity of the Tower of Hanoi, we tested Hanoi-iiwa’s performance on the 3-disk Tower of Hanoi puzzle. Our simulation showed that Hanoi-iiwa was able to successfully solve the puzzle 100% of the time over 10 runs. In terms of efficiency, Hanoi-iiwa was able to solve the puzzle in the minimum number of steps (7), but it took 175 seconds to complete those steps, averaging 25 seconds per step. Overall, Hanoi-iiwa meets our design goal of generating correct puzzle solutions and performing efficient task planning. It offers a straightforward framework for combining task planning and motion planning to enable robots to solve mathematical puzzles. However, there is room for improvement in terms of the time-efficiency of manipulation.